生命游戏

问题

根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

1. 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
2. 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
3. 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
4. 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

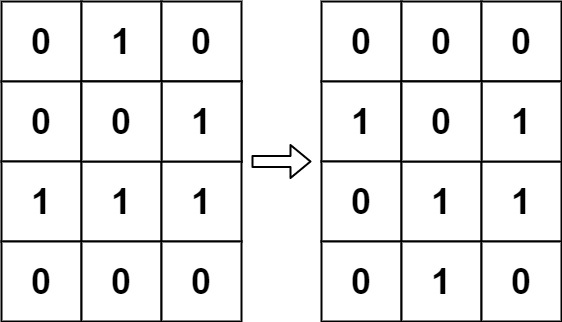
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

示例 1：

输入： board = [0,1,0],[0,0,1],[1,1,1],0,0,0 输出：[0,0,0],[1,0,1],[0,1,1],0,1,0

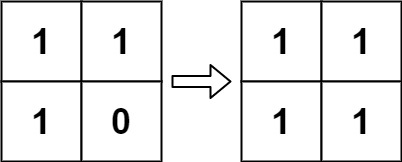
示例 2：

**输入：**board = [1,1],1,0 输出：[1,1],1,1

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 25
• board[i][j] 为 0 或 1

进阶：

• 你可以使用原地算法解决本题吗？请注意，面板上所有格子需要同时被更新：你不能先更新某些格子，然后使用它们的更新后的值再更新其他格子。
• 本题中，我们使用二维数组来表示面板。原则上，面板是无限的，但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题？

方法一

解题思路

1. 构建board副本数组
2. 统计副本数组中每个细胞周围的其他细胞（未更新）状态
3. 更新每个细胞的状态，即一次更新后的细胞（board数组）

副本构造

// 数组副本
const CopyBoard = board.map(ary => {
    // 值是基础类型（Number），不存在引用问题，直接解构比较方便
    return [...ary];
});

状态统计

在之前的“每日一题”活动中，这类的问题非常常见，比如车的可用捕获量，一般常见的做法，都是利用坐标数组进行遍历，提高解题的灵活性。

首先，将board抽象成由X（行）和Y（列）组成，则X（行）设定为西——>东方向，Y（列）设定为北——>南方向。即上北，下南，左西，右东，则x表示在X上的位置，y表示在Y上的位置。

很轻易地可以总结出：

• (0 + x, 1 + y)：x坐标不变，y前进一格，则是由西向东移动。
• (1 + x, 0 + y)：x坐标前进一格，y不变，则是由北向南移动。
• (0 + x, -1 + y)：x坐标不变，y后退一格，则是由东向西移动。
• (-1 + x, 0 + y)：x坐标后退一格，y不变，则是由南向北移动。
• (-1 + x, -1 + y)：x，y各后退一格，即向西北方向的对角线移动。
• (-1 + x, 1 + y)：x坐标后退一格，y坐标前进一格，即向东北方向的对角线移动。
• (1 + x, 1 + y)：x，y各前进一格，即向东南方向的对角线移动。
• (1 + x, -1 + y)：x坐标前进一格，y坐标后退一格，即向西南方向的对角线移动。

把上述的坐标由上到下，将加号“+”视为分割线，你会发现，x的位置移动，由数组[0, 1, 0, -1, -1, -1, 1, 1]构成，y的位置移动，由[1, 0, -1, 0, 1, -1, 1, -1]构成，这样一来，方向坐标就确立了。

方向数组的确定，给解题带来极大的便利，无需手动判断八个位置，只需要遍历坐标数组一次，就可以统计出坐标(i, j)细胞周边的细胞存活量。

// 方向数组
const idx = [0, 1, 0, -1, -1, -1, 1, 1];
const jdx = [1, 0, -1, 0, 1, -1, 1, -1];
 
// 利用双重循环保证每个细胞都走一遍
for(let i = 0; i < CopyBoard.length; i++) {
    for(let j = 0; j < CopyBoard[i].length; j++) {
        
        // 遍历方向坐标数组
        for(let index = 0; index < 8; index++) {
            let x = i + idx[index];
            let y = j + jdx[index];
            ...
        }
    }
}  

细胞状态更新

// 该位置细胞死活状态决策
if(liveAmount < 2 || liveAmount > 3) {
    board[i][j] = 0;
} else if (liveAmount <= 3 && CopyBoard[i][j]) {
    board[i][j] = 1;
} else if (liveAmount === 3 && !CopyBoard[i][j]) {
    board[i][j] = 1;
}

代码实现

/**
 * @param {number[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
var gameOfLife = function(board) {
    // 八个方向的偏移量
    const idx = [0, 1, 0, -1, -1, -1, 1, 1];
    const jdx = [1, 0, -1, 0, 1, -1, 1, -1];
 
    // 数组副本
    const CopyBoard = board.map(ary => {
        // 值是基础类型（Number），不存在引用问题，直接解构比较方便
        return [...ary];
    });
 
 
    // 遍历每个细胞
    for(let i = 0; i < CopyBoard.length; i++) {
        for(let j = 0; j < CopyBoard[i].length; j++) {
            
            // 周边活细胞统计
            let liveAmount = 0;
 
            // 八个方向都走一遍
            for(let index = 0; index < 8; index++) {
                let x = i + idx[index];
                let y = j + jdx[index];
 
                // 边界规避
                if(x < 0 || y < 0 || x >= CopyBoard.length || y >= CopyBoard[i].length) continue;
                
                // 活细胞则计数加1
                liveAmount += CopyBoard[x][y] ? 1 : 0;
            }
 
            // 该位置细胞死活决策
            if(liveAmount < 2 || liveAmount > 3) {
                board[i][j] = 0;
            } else if (liveAmount <= 3 && CopyBoard[i][j]) {
                board[i][j] = 1;
            } else if (liveAmount === 3 && !CopyBoard[i][j]) {
                board[i][j] = 1;
            }
        }
    }
};

方法二： 哈希表

解题思路

• 直接改board，会影响后续判断。用哈希表h存改动过的位置。取值时，如果该位置被改动过取反
• 取值时，越界返回0。活细胞数量判断时，只关心能改变细胞状态的条件。改动位置存哈希表
• 本题只需一次双循环遍历二维数组。根据是否有改动，有改动重复双循环，还可求解最终稳定状态

var gameOfLife = function(board) {
    var v = (i, j) => board[i] ? (h[i + ',' + j] ? board[i][j] ^ 1 : board[i][j] || 0) : 0, h = {}
    for (var i = 0; i < board.length; i++) 
        for (var j = 0; j < board[i].length; j++) {
            var alive = v(i, j - 1) + v(i - 1, j - 1) + v(i - 1, j) + v(i - 1, j + 1) +
                        v(i, j + 1) + v(i + 1, j - 1) + v(i + 1, j) + v(i + 1, j + 1) 
                if (alive < 2 || alive > 3) {
                    if (board[i][j] === 1) board[i][j] = 0, h[i + ',' +j] = 1
                } else if (alive === 3) {
                    if (board[i][j] === 0) board[i][j] = 1, h[i + ',' +j] = 1
                }
        }
};

注意❗

需要注意 ^ 为 异或运算符 中的异或运算符，若两个二进制位不相同，则结果为1，否则为0。