你可能听说过函数式编程(Functional programming),甚至已经使用了一段时间。
但是,你能说清楚,它到底是什么吗?

网上搜索一下,你会轻松找到好多答案。
- 与面向对象编程(Object-oriented programming)和过程式编程(Procedural programming)并列的编程范式。
- 最主要的特征是,函数是第一等公民。
- 强调将计算过程分解成可复用的函数,典型例子就是
map方法和reduce方法组合而成 MapReduce 算法。 - 只有纯的、没有副作用的函数,才是合格的函数。
上面代码中, 这些说法都对,但还不够,都没有回答下面这个更深层的问题。

为什么要这样做?
这就是,本文要解答的问题。我会通过最简单的语言,帮你理解函数式编程,并且学会它那些基本写法。
需要声明的是,我不是专家,而是一个初学者,最近两年才真正开始学习函数式编程。一直苦于看不懂各种资料,立志要写一篇清晰易懂的教程。下面的内容肯定不够严密,甚至可能包含错误,但是我发现,像下面这样解释,初学者最容易懂。
一、范畴论
函数式编程的起源,是一门叫做范畴论(Category Theory)的数学分支。

理解函数式编程的关键,就是理解范畴论。它是一门很复杂的数学,认为世界上所有的概念体系,都可以抽象成一个个的”范畴”(category)。
1.1 范畴的概念
什么是范畴呢?
维基百科的一句话定义如下。
“范畴就是使用箭头连接的物体。“(In mathematics, a category is an algebraic structure that comprises “objects” that are linked by “arrows”. )
也就是说,彼此之间存在某种关系的概念、事物、对象等等,都构成”范畴”。随便什么东西,只要能找出它们之间的关系,就能定义一个”范畴”。

上图中,各个点与它们之间的箭头,就构成一个范畴。
箭头表示范畴成员之间的关系,正式的名称叫做”态射”(morphism)。范畴论认为,同一个范畴的所有成员,就是不同状态的”变形”(transformation)。通过”态射”,一个成员可以变形成另一个成员。
1.2 数学模型
既然”范畴”是满足某种变形关系的所有对象,就可以总结出它的数学模型。
- 所有成员是一个集合
- 变形关系是函数
也就是说,范畴论是集合论更上层的抽象,简单的理解就是”集合 + 函数”。
理论上通过函数,就可以从范畴的一个成员,算出其他所有成员。
1.3 范畴与容器
我们可以把”范畴”想象成是一个容器,里面包含两样东西。
- 值(value)
- 值的变形关系,也就是函数。
下面我们使用代码,定义一个简单的范畴。
class Category {
constructor(val) {
this.val = val;
}
addOne(x) {
return x + 1;
}
}上面代码中,Category是一个类,也是一个容器,里面包含一个值(this.val)和一种变形关系(addOne)。你可能已经看出来了,这里的范畴,就是所有彼此之间相差1的数字。
注意❗
注意,本文后面的部分,凡是提到”容器”的地方,全部都是指”范畴”。
1.4 范畴论与函数式编程的关系
范畴论使用函数,表达范畴之间的关系。
伴随着范畴论的发展,就发展出一整套函数的运算方法。这套方法起初只用于数学运算,后来有人将它在计算机上实现了,就变成了今天的”函数式编程”。
本质上,函数式编程只是范畴论的运算方法,跟数理逻辑、微积分、行列式是同一类东西,都是数学方法,只是碰巧它能用来写程序。
所以,你明白了吗,为什么函数式编程要求函数必须是纯的,不能有副作用?因为它是一种数学运算,原始目的就是求值,不做其他事情,否则就无法满足函数运算法则了。
总之,在函数式编程中,函数就是一个管道(pipe)。这头进去一个值,那头就会出来一个新的值,没有其他作用。
二、函数的合成与柯里化
函数式编程有两个最基本的运算:合成和柯里化。
2.1 函数的合成
如果一个值要经过多个函数,才能变成另外一个值,就可以把所有中间步骤合并成一个函数,这叫做”函数的合成”(compose)。
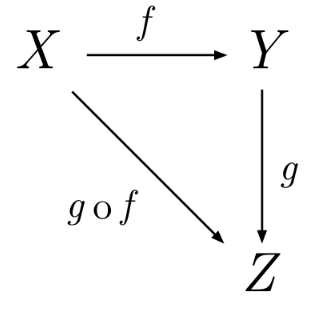
上图中,X和Y之间的变形关系是函数f,Y和Z之间的变形关系是函数g,那么X和Z之间的关系,就是g和f的合成函数g·f。
下面就是代码实现了,我使用的是 JavaScript 语言。注意,本文所有示例代码都是简化过的,完整的 Demo 请看《参考链接》部分。
合成两个函数的简单代码如下。
const compose = function (f, g) {
return function (x) {
return f(g(x));
};
}函数的合成还必须满足结合律。
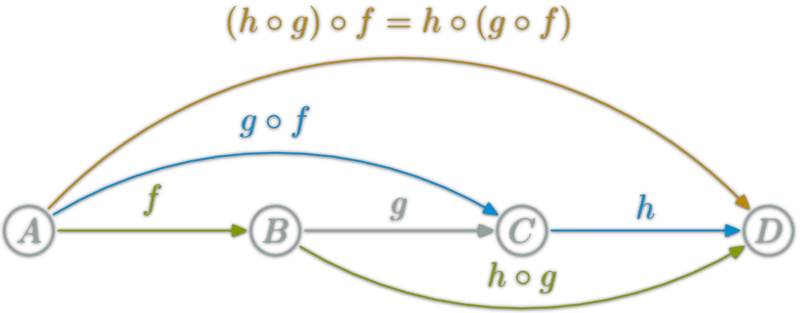
compose(f, compose(g, h))
// 等同于
compose(compose(f, g), h)
// 等同于
compose(f, g, h)合成也是函数必须是纯的一个原因。因为一个不纯的函数,怎么跟其他函数合成?怎么保证各种合成以后,它会达到预期的行为?
前面说过,函数就像数据的管道(pipe)。那么,函数合成就是将这些管道连了起来,让数据一口气从多个管道中穿过。
2.2 柯里化
f(x)和g(x)合成为f(g(x)),有一个隐藏的前提,就是f和g都只能接受一个参数。如果可以接受多个参数,比如f(x, y)和g(a, b, c),函数合成就非常麻烦。
这时就需要函数柯里化了。所谓”柯里化”,就是把一个多参数的函数,转化为单参数函数。
// 柯里化之前
function add(x, y) {
return x + y;
}
add(1, 2) // 3
// 柯里化之后
function addX(y) {
return function (x) {
return x + y;
};
}
addX(2)(1) // 3有了柯里化以后,我们就能做到,所有函数只接受一个参数。后文的内容除非另有说明,都默认函数只有一个参数,就是所要处理的那个值。
三、函子
函数不仅可以用于同一个范畴之中值的转换,还可以用于将一个范畴转成另一个范畴。这就涉及到了函子(Functor)。
3.1 函子的概念
函子是函数式编程里面最重要的数据类型,也是基本的运算单位和功能单位。
它首先是一种范畴,也就是说,是一个容器,包含了值和变形关系。比较特殊的是,它的变形关系可以依次作用于每一个值,将当前容器变形成另一个容器。
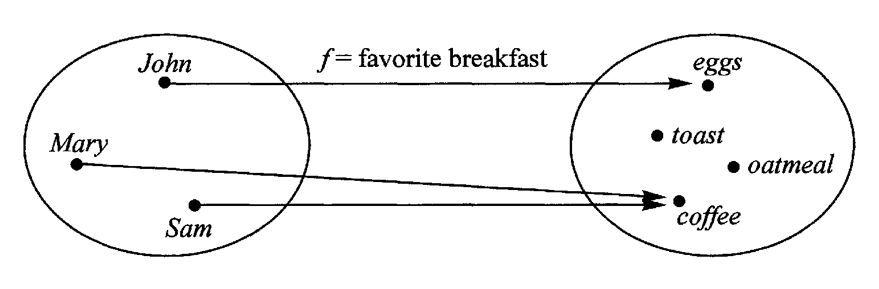
上图中,左侧的圆圈就是一个函子,表示人名的范畴。外部传入函数f,会转成右边表示早餐的范畴。
下面是一张更一般的图。

上图中,函数f完成值的转换(a到b),将它传入函子,就可以实现范畴的转换(Fa到Fb)。
3.2 函子的代码实现
任何具有map方法的数据结构,都可以当作函子的实现。
class Functor {
constructor(val) {
this.val = val;
}
map(f) {
return new Functor(f(this.val));
}
}上面代码中,Functor是一个函子,它的map方法接受函数f作为参数,然后返回一个新的函子,里面包含的值是被f处理过的(f(this.val))。
一般约定,函子的标志就是容器具有map方法。该方法将容器里面的每一个值,映射到另一个容器。
下面是一些用法的示例。
(new Functor(2)).map(function (two) {
return two + 2;
});
// Functor(4)
(new Functor('flamethrowers')).map(function(s) {
return s.toUpperCase();
});
// Functor('FLAMETHROWERS')
(new Functor('bombs')).map(_.concat(' away')).map(_.prop('length'));
// Functor(10)上面的例子说明,函数式编程里面的运算,都是通过函子完成,即运算不直接针对值,而是针对这个值的容器----函子。函子本身具有对外接口(map方法),各种函数就是运算符,通过接口接入容器,引发容器里面的值的变形。
因此,学习函数式编程,实际上就是学习函子的各种运算。 由于可以把运算方法封装在函子里面,所以又衍生出各种不同类型的函子,有多少种运算,就有多少种函子。函数式编程就变成了运用不同的函子,解决实际问题。
四、of 方法
你可能注意到了,上面生成新的函子的时候,用了new命令。这实在太不像函数式编程了,因为new命令是面向对象编程的标志。
函数式编程一般约定,函子有一个of方法,用来生成新的容器。
下面就用of方法替换掉new。
Functor.of = function(val) {
return new Functor(val);
};然后,前面的例子就可以改成下面这样。
Functor.of(2).map(function (two) {
return two + 2;
});
// Functor(4)这就更像函数式编程了。
五、Maybe 函子
函子接受各种函数,处理容器内部的值。这里就有一个问题,容器内部的值可能是一个空值(比如null),而外部函数未必有处理空值的机制,如果传入空值,很可能就会出错。
Functor.of(null).map(function (s) {
return s.toUpperCase();
});
// TypeError上面代码中,函子里面的值是null,结果小写变成大写的时候就出错了。
Maybe 函子就是为了解决这一类问题而设计的。简单说,它的map方法里面设置了空值检查。
class Maybe extends Functor {
map(f) {
return this.val ? Maybe.of(f(this.val)) : Maybe.of(null);
}
}有了 Maybe 函子,处理空值就不会出错了。
Maybe.of(null).map(function (s) {
return s.toUpperCase();
});
// Maybe(null)六、Either 函子
条件运算if...else是最常见的运算之一,函数式编程里面,使用 Either 函子表达。
Either 函子内部有两个值:左值(Left)和右值(Right)。右值是正常情况下使用的值,左值是右值不存在时使用的默认值。
class Either extends Functor {
constructor(left, right) {
this.left = left;
this.right = right;
}
map(f) {
return this.right ?
Either.of(this.left, f(this.right)) :
Either.of(f(this.left), this.right);
}
}
Either.of = function (left, right) {
return new Either(left, right);
};下面是用法。
var addOne = function (x) {
return x + 1;
};
Either.of(5, 6).map(addOne);
// Either(5, 7);
Either.of(1, null).map(addOne);
// Either(2, null);上面代码中,如果右值有值,就使用右值,否则使用左值。通过这种方式,Either 函子表达了条件运算。
Either 函子的常见用途是提供默认值。下面是一个例子。
Either
.of({address: 'xxx'}, currentUser.address)
.map(updateField);上面代码中,如果用户没有提供地址,Either 函子就会使用左值的默认地址。
Either 函子的另一个用途是代替try...catch,使用左值表示错误。
function parseJSON(json) {
try {
return Either.of(null, JSON.parse(json));
} catch (e: Error) {
return Either.of(e, null);
}
}上面代码中,左值为空,就表示没有出错,否则左值会包含一个错误对象e。一般来说,所有可能出错的运算,都可以返回一个 Either 函子。
七、ap 函子
函子里面包含的值,完全可能是函数。我们可以想象这样一种情况,一个函子的值是数值,另一个函子的值是函数。
function addTwo(x) {
return x + 2;
}
const A = Functor.of(2);
const B = Functor.of(addTwo)上面代码中,函子 代码中,函子A内部的值是2,函子B内部的值是函数addTwo。
有时,我们想让函子B内部的函数,可以使用函子A内部的值进行运算。这时就需要用到 ap 函子。
ap 是 applicative(应用)的缩写。凡是部署了ap方法的函子,就是 ap 函子。
class Ap extends Functor {
ap(F) {
return Ap.of(this.val(F.val));
}
}注意❗
注意,
ap方法的参数不是函数,而是另一个函子。
因此,前面例子可以写成下面的形式。
Ap.of(addTwo).ap(Functor.of(2))
// Ap(4)ap 函子的意义在于,对于那些多参数的函数,就可以从多个容器之中取值,实现函子的链式操作。
function add(x) {
return function (y) {
return x + y;
};
}
Ap.of(add).ap(Maybe.of(2)).ap(Maybe.of(3));
// Ap(5)上面代码中,函数add是柯里化以后的形式,一共需要两个参数。通过 ap 函子,我们就可以实现从两个容器之中取值。它还有另外一种写法。
Ap.of(add(2)).ap(Maybe.of(3));八、Monad 函子
函子是一个容器,可以包含任何值。函子之中再包含一个函子,也是完全合法的。但是,这样就会出现多层嵌套的函子。
Maybe.of(
Maybe.of(
Maybe.of({name: 'Mulburry', number: 8402})
)
)上面这个函子,一共有三个Maybe嵌套。如果要取出内部的值,就要连续取三次this.val。这当然很不方便,因此就出现了 Monad 函子。
Monad 函子的作用是,总是返回一个单层的函子。 它有一个flatMap方法,与map方法作用相同,唯一的区别是如果生成了一个嵌套函子,它会取出后者内部的值,保证返回的永远是一个单层的容器,不会出现嵌套的情况。
class Monad extends Functor {
join() {
return this.val;
}
flatMap(f) {
return this.map(f).join();
}
}上面代码中,如果函数f返回的是一个函子,那么this.map(f)就会生成一个嵌套的函子。所以,join方法保证了flatMap方法总是返回一个单层的函子。这意味着嵌套的函子会被铺平(flatten)。
九、IO 操作
Monad 函子的重要应用,就是实现 I/O (输入输出)操作。
I/O 是不纯的操作,普通的函数式编程没法做,这时就需要把 IO 操作写成Monad函子,通过它来完成。
var fs = require('fs');
var readFile = function(filename) {
return new IO(function() {
return fs.readFileSync(filename, 'utf-8');
});
};
var print = function(x) {
return new IO(function() {
console.log(x);
return x;
});
}上面代码中,读取文件和打印本身都是不纯的操作,但是readFile和print却是纯函数,因为它们总是返回 IO 函子。
如果 IO 函子是一个Monad,具有flatMap方法,那么我们就可以像下面这样调用这两个函数。
readFile('./user.txt')
.flatMap(print)这就是神奇的地方,上面的代码完成了不纯的操作,但是因为flatMap返回的还是一个 IO 函子,所以这个表达式是纯的。我们通过一个纯的表达式,完成带有副作用的操作,这就是 Monad 的作用。
由于返回还是 IO 函子,所以可以实现链式操作。因此,在大多数库里面,flatMap方法被改名成chain。
var tail = function(x) {
return new IO(function() {
return x[x.length - 1];
});
}
readFile('./user.txt')
.flatMap(tail)
.flatMap(print)
// 等同于
readFile('./user.txt')
.chain(tail)
.chain(print)上面代码读取了文件user.txt,然后选取最后一行输出。